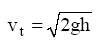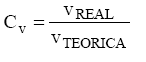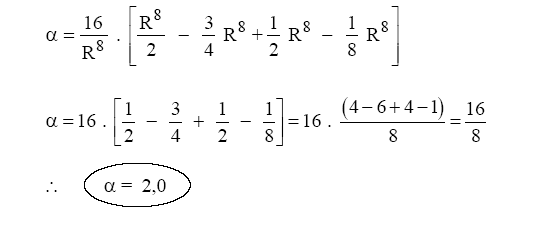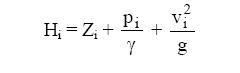5.6.2.5 Medidor Tipo Placa de Orifício

O medidor tipo placa de orifício ou diafragma é constituído por uma placa delgada, na qual se abre um orifício e é utilizado em conduto forçado figura (5.22).

Como a geometria deste tipo de medidor é simples, apresenta um custo baixo ao ser comparado com o tipo Venturi, porém a expansão descontrolada a sua jusante acarreta elevada dissipação de energia figura (5.23).

Devemos notar que a tomada de pressão para as placas de orifício influenciam nos coeficientes de correção usados, sendo que inicialmente consideramos a situação representada pela figura 5.22 . Temos : C_C ≠ 1,0 ; A_mín = A₀ e C_d = C_V . C_C e isto nos permite reescrever a equação 5.24, obtendo a equação para o medidor tipo placa de orifício (equação 5.28).

Para se obter resultados precisos com o medidor tipo placa de orifício, o mesmo deve ser instalado no mínimo a 40 x D_tubo à jusante de uma singularidade, se a mesma existir. Ao analisarmos a equação 5.28, verificamos que a sua utilização apresenta certa dificuldade, principalmente no que se refere a obtenção de C_C , por este motivo introduz-se um novo coeficiente de correção, que é denominado de coeficiente de escoamento e comumente representado por C, o qual é obtido experimentalmente e é função do número de Reynolds de aproximação (Re₁) e da relação D₀/D₁ (figura 5.24).

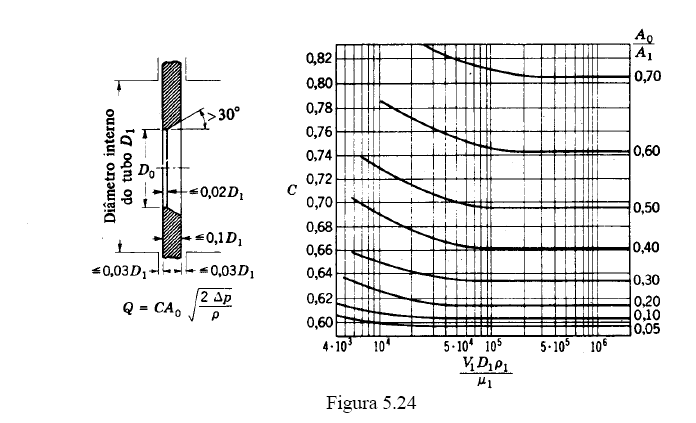
O coeficiente de escoamento (C) é definido pela equação 5.29.

Através da equação 5.29, obtemos a nova equação para a determinação de vazão real do medidor tipo placa de orifício (equação 5.30).

Na escolha de um medidor de vazão, devemos considerar os seguintes ítens:

• custo;

• precisão de leitura;

• a necessidade de calibração;

• a facilidade tanto da instalação como da manutenção.

Atualmente após a análise dos itens mencionados anteriormente, podemos afirmar que geralmente a escolha é feita pelos medidores tipo placa de orifício (diafragma), por este motivo mencionamos que existe um trabalho baseado na norma ISO 5167 cuja primeira edição data de 1980, que esta sendo adaptado pela ABNT e que é básico para a determinação dos coeficientes de correção deste aparelho.

Em futuras edições, apresentaremos um resumo deste trabalho.

5.6.2.6 Bocais de Fluxo

Este tipo de medidor de vazão é praticamente intermediário, tanto em relação à custo, como em relação a dissipação de energia comparado ao tipo Venturi e ao tipo placa de orifício.

O inesquecível Professor Azevedo Neto (Em seu livro – Manual de Hidráulica – editado pela Editora Edgard Blücher Ltda – na 7ª edição página 66) define de uma forma clara os bocais:

“Os bocais ou tubos adicionais são constituídos por peças tubulares adaptadas aos orifícios. Servem para dirigir o jato. O seu comprimento deve estar compreendido entre vez e meia (1,5) e três (3,0) vezes o seu diâmetro. De um modo geral, e para comprimentos maiores, consideram-se comprimentos de 1,5 a 3,0D como bocais, de 3,0 a 500D como tubos muito curtos; de 500 a 4000D (aproximadamente) como tubulações curtas; e acima de 4000D como tubulações longas.” Os bocais geralmente são classificados em : cilindros (interiores ou reentrantes) e exteriores - cônicos (convergentes e divergentes).

As figuras 5.25 e 5.26 representam exemplo de bocal cilíndrico e cônico respectivamente.

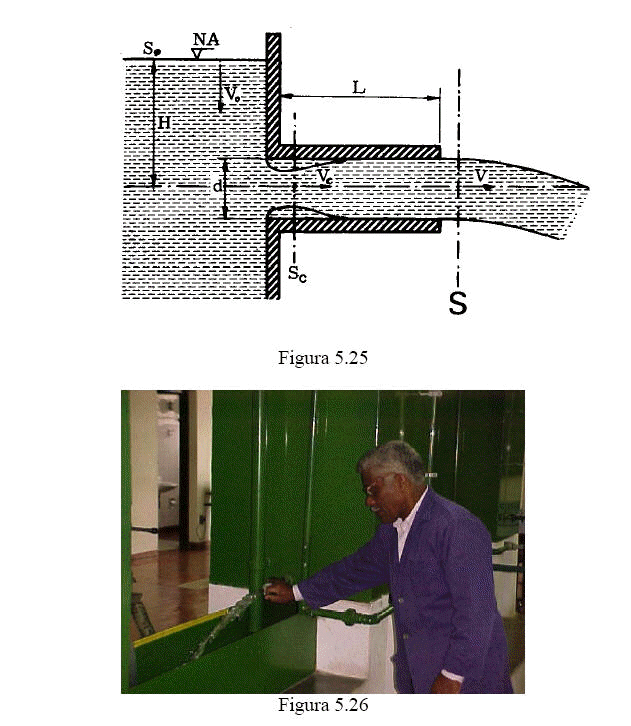
Considerando o bocal instalado em um reservatório (figura 5.26) a determinação do seu coeficiente de velocidade é análoga a apresentada para a determinação da equação 5.15 e 5.16, respectivamente:

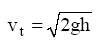
Onde:

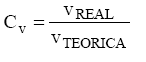
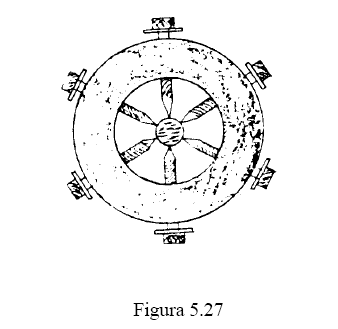
Já a determinação do coeficiente de contração se for experimental, consiste na determinação da área contraída (AC) por intermédio de parafusos “CALANTES” solitários a uma coroa suporte (figura 5.27), que deve ser instalada a uma distância L.

Salientamos que esta maneira apresentada para a determinação da área contraída é bastante imprecisa, devendo ser substituída por outro método, onde o mais comum consiste na determinação do C_V, como o mencionado, e na determinação do coeficiente de vazão (C_d) e a partir daí a determinação de C_C pela equação 5.31.

Considerando o bocal instalado no interior da tubulação, nesta situação, voltamos a usar o coeficiente de escoamento (K) e a situação é representada pela figura 5.29, onde a pressão p₁ é medida a uma distância D₁ à montante do bocal e a pressão p₂ quando termina o bocal.

Como C_C = 1,0 , podemos especificar o coeficiente de escoamento (K) pela equação 5.32 .

Devemos notar que os valores de K > 1,0 , são devido ao denominador ser menor que 1,0. O gráfico representado pela figura 5.30, mostra K = f (Re₁) , onde salientamos que para Reynolds de aproximação maiores à cerca de 2 x 10⁵ observa-se que o K permanece constante.

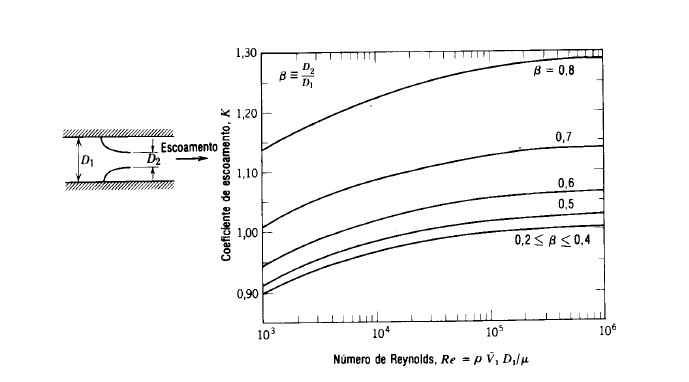
Figura 5.30

5.7 Conceitos de Perda de Carga e do Coeficiente de Energia Cinética

A principal limitação da equação de Bernoulli está em considerar o escoamento de um fluido ideal, ou seja, aquele que apresenta viscosidade nula, o que implica dizer que não há dissipação de energia ao longo do escoamento.

A partir deste ponto, iremos eliminar esta hipótese, ou seja consideraremos o escoamento de um fluido real (µ ≠ 0), o que implica dizer que iremos considerar a dissipação de energia ao longo do escoamento.

Define-se perda de carga, que geralmente é representado por Hp, como sendo a dissipação de energia por unidade de peso.

Outro fato importante a se considerar: pelo fato da viscosidade ser diferente de zero tem-se o diagrama de velocidade, nas seções do escoamento, não uniforme, o que implica que a carga cinética calculada por v²/2g, pode conter erro, principalmente quando tivermos um escoamento laminar. Para sua correção deve-se calculá-la por: av²/2g, onde a é um coeficiente de correção denominado de coeficiente de energia cinética.

O coeficiente de energia cinética é definido da seguinte forma:

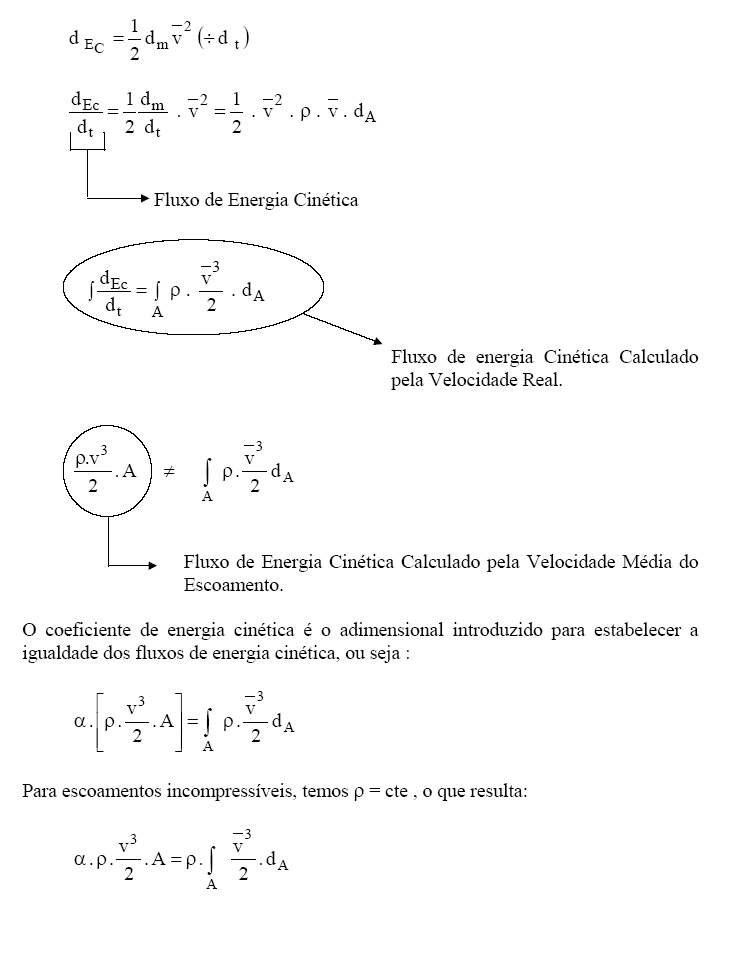
Portanto:

Como os condutos forçados de seção transversal circular representam um número grande de aplicações, vamos analisá-los para os seguintes casos:

1º - escoamento laminar:

Portanto:

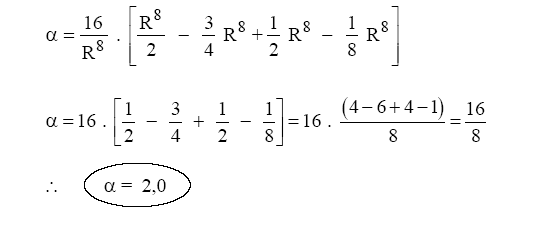
CONCLUSÃO: Para os condutos forçados de seção transversal circular com escoamento laminar a carga cinética será calculada por v²/g; portanto neste caso, temos:

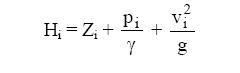
2º - escoamento turbulento

Portanto:

5.8 Conceito de Máquinas Hidráulicas

Consideramos máquina hidráulica o dispositivo que fornece ou retira energia do fluido.

Ao considerarmos que a energia, é fornecida ou retirada, por unidade de peso, estaremos definindo a carga ou altura manométrica da máquina hidráulica, que é representada por Hm.

5.9 Classificação Básica das Máquinas Hidráulicas

A classificação básica será feita em relação a máquina fornecer, retirar ou transformar energia do fluido, por outro lado, devemos lembrar que o nosso estudo é dirigido para o escoamento considerado incompressível, o que implica que a classificação básica apresentada considera também esta restrição.

• Máquinas Geratrizes - são aquelas que recebem trabalho mecânico e o transforma em energia fluida. Podemos citar como exemplos de máquinas geratrizes as bombas hidráulicas e os ventiladores. No nosso curso só estudamos os princípios básicos das bombas hidráulicas.

• Máquinas Motrizes - são aquelas que transformam a energia fluida em energia mecânica. Podemos citar como exemplo de máquinas motrizes as turbinas hidráulicas.

• Máquinas Mistas - são os dispositivos que modificam a energia que o fluido possui. Podemos citar como exemplos de máquinas mistas os ejetores e os carneiros hidráulicos.

Clique na figura acima e assista ao vídeo

5.10 Equação da Energia para o Escoamento Unidirecional Incompressível e em Regime Permanente

5.10.1 Instalações básicas: com apenas uma entrada e uma saída e sem presença de máquina hidráulica

Nesta condição, podemos afirmar que o fluido escoa espontaneamente da carga total maior para a carga total menor. Considerando o trecho de uma instalação hidráulica, representado pela figura 5.31, podemos efetuar o balanço de energias, proposto pela equação da energia.

Nota: O único trecho de uma instalação hidráulica, onde não consideramos a perda de carga, é entre a entrada e saída que uma máquina hidráulica, isto porque as perdas já são consideradas no rendimento da máquina, que é sempre menor do que 1,0.

5.10.2 Com apenas uma Entrada e uma Saída na Presença de Máquina Hidráulica

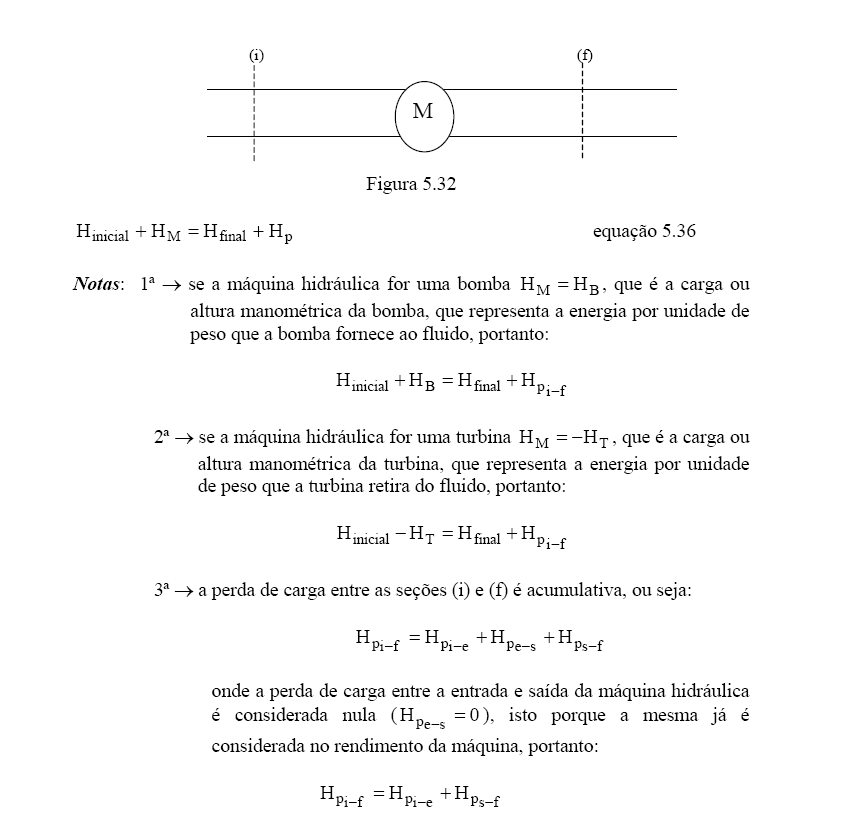
Considerando o trecho de uma instalação hidráulica, que é representado pela figura 5.32, podemos efetuar o balanço de energias entre a seções (i) e (f), que origina a equação 5.36.