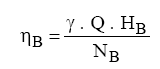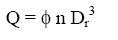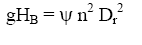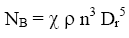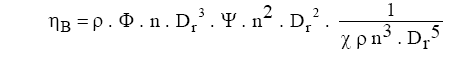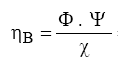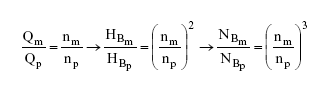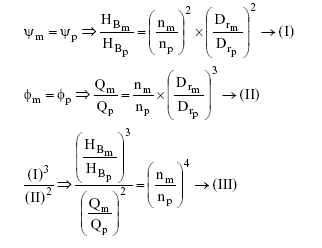Análise dimensional e leis de semelhança aplicadas as bombas hidráulicas.
Para os escoamentos incompressíveis, pode-se considerar o fenômeno definido pela seguinte função característica: f (NB, Dr, n, Q, γ HB, ρ, µ) = 0, onde aplicando-se o teorema de Buckingham (ou "pi = p") tem-se:
-
coeficiente manométrico:
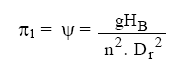
-
coeficiente de vazão:

-
coeficiente de potência:
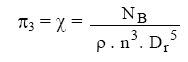
-
adimensional proporcional ao número de Reynolds:
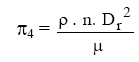
Por outro lado, evocando-se a expressão para o cálculo do rendimento da bomba, tem-se:
Através das expressões a seguir que foram originadas dos adimensionais típicos das bombas hidráulicas, pode-se obter uma importante relação entre o rendimento da bomba e estes adimensionais típicos:
Portanto:
Nota: Pelo fato do coeficiente manométrico (Y) e do coeficiente de potência (c) serem função do coeficiente de vazão (F), pode-se concluir que o rendimento da bomba também o será, ou seja: hB = f(F)
Como na condição de semelhança completa tem-se que: Fm = Fp ; Ym = Yp e cm = cp pode-se concluir que também fará parte das condições de semelhança a igualdade entre os rendimentos das bombas, ou seja: hm = hp. "Na prática as bombas maiores são mais eficientes, tendo um número de Reynolds maior e razões de rugosidade e de folga menores. Duas correlações empíricas são recomendadas para o rendimento máximo. Uma desenvolvida por Moody para turbinas, mas utilizada também para bombas, representa o efeito do tamanho. A outra, sugerida por Anderson a partir de milhares de testes de bombas, representa o efeito da vazão." (White, Frank M. - Mecânica dos Fluidos - Mc Graw Hill - p.504)

A igualdade hm = hp foi utilizada na experiência do inversor de freqüência, onde estudou-se o efeito da mudança de rotação nas curvas características da bomba hidráulica. Apesar da igualdade ter sido usada, é importante mencionar que se pode calcular o rendimento pela expressão empírica, onde o índice "x" indica a bomba com a nova rotação. (Macintyre, Archibald Joseph - Bombas e Instalações de Bombeamento - editado pela Guanabara Dois - segunda edição)
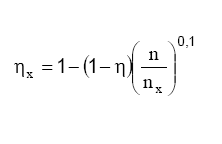
Para justificar a importância do estudo do inversor de freqüência, deve-se lembrar que uma das maneiras de alterar o ponto de trabalho de uma bomba hidráulica é através do fechamento de uma válvula hidráulica, porém este procedimento é menos eficiente, do ponto de vista econômico, do que operar com inversor de freqüência, onde alterando-se a rotação deve-se efetuar a correção das curvas características através das expressões oriundas das condições de semelhança, ou seja:
Outro ponto a ser observado é que existem muitos tipos de bomba e cada um deles com suas características geométricas, atendendo uma faixa de vazões e de cargas, portanto na escolha da bomba, além dela atender o par HB e Q, deve operar com o melhor rendimento possível e para isto, deve-se escolher a geometria conveniente para uma dada instalação.
Para a escolha da bomba adequada, uma das possibilidades é se recorrer a rotação específica, que é uma expressão matemática oriunda das condições de semelhança.
Para a determinar da rotação específica é conveniente se introduzir o conceito de bomba unidade, que a bomba que irá operar com uma rotação nq, com uma vazão Q = 1 m³/h e com HB = 1 m.
Partindo das condições de semelhança, obtém-se as equações:
Observe-se que a equação (III) utiliza a vazão, a carga e a rotação de duas bombas pertencentes a uma mesma família, na condição especial de semelhança completa.
Para generalizar a situação anterior, optou-se em considerar como modelo a bomba unidade, que passa a ser um modelo que vale para qualquer família, onde tanto a vazão como a carga manométrica são definidas para o ponto de projeto, ou seja, o ponto onde se tem o rendimento máximo, o qual pode coincidir, ou não, com o ponto de trabalho.
Considerando a bomba unidade como modelo, pode-se reescrever a equação (III) que dará origem a expressão para o cálculo da rotação específica:
Deve-se notar que com as características n, Q e HB de uma bomba real, os dois últimos obtidos para a condição de ponto de projeto, ou seja, para o rendimento máximo, pode-se calcular a rotação específica, a qual possibilita conhecer a classificação das bombas segundo o seu tipo de rotor:
| nq (rpm) | Tipo de bomba (rotor) |
| < 10 | Deslocamento positivo - êmbolo, engrenagens, lóbulos, parafusos, palhetas, etc. |
| 10 a 40 | Centrífuga radial ou pura |
| 35 a 85 | Centrífuga tipo Francis, ou seja, a helicoidal. |
| 80 a 150 | Centrífuga de fluxo misto ou semi-axial |
| 125 a 500 | Axial |
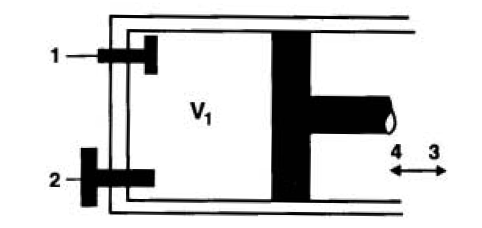
Bombas de deslocamento positivo: este tipo de máquina tem por
característica de funcionamento a transferência direta da energia
mecânica cedida pela fonte motora em energia potencial (energia de
pressão). Esta transferência é obtida pela movimentação de um órgão
mecânico da bomba, que obriga o fluido a executar o mesmo movimento do
qual ele está animado.
O líquido, sucessivamente enche e depois é expulso dos espaços com
volume determinado no interior da bomba, dai resultando o nome de bombas
volumétricas.
As bombas de deslocamento positivo podem se dividas em bombas de êmbolo ou alternativas e bombas rotativas

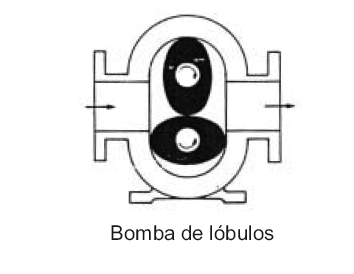
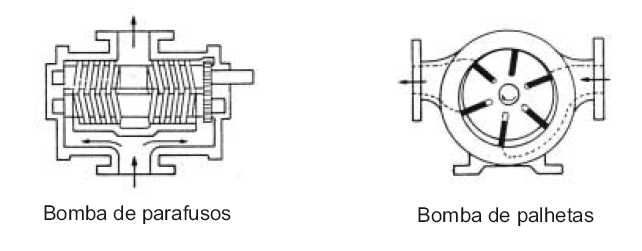
Bombas centrífugas: este tipo de bomba tem por princípio de funcionamento a transferência de energia mecânica para o fluido a ser bombeado em forma de energia cinética. Por sua vez, esta energia cinética é transformada em energia potencial ( energia de pressão ) sendo esta a sua característica principal. O movimento rotacional de um rotor inserido em uma carcaça (corpo da bomba ) é o orgão funcional responsável por tal transformação.
Classificação:
a) Radiais ou Puras: quando a direção do fluido bombeado é perpendicular ao eixo de rotação.
b) Fluxo misto ou Semi-Axial: quando a direção do fluido bombeado é inclinada em relação ao eixo de rotação.
c) Fluxo Axial: quando a direção do fluido bombeado é paralela em relação ao eixo de rotação.

Notas:
-
Rotação específica americana, ou seja, quando a carga manométrica (HB) é igual a 1 pé, a vazão (Q) igual a 1 gpm, neste caso tem-se que: nqUSA = 52nq métrico
-
Rotação específica com potência unitária (nS), ou seja, N = 1 CV, isto implica que Q = 75 l/s, portanto: nS=3,65nq
-
A fabrica de bombas KSB, em função das condições operacionais (n, Q e HB) e da rotação específica, mostra através do gráfico a seguir a determinação do tipo de rotor e do rendimento máximo esperado. Deve-se notar que o referido gráfico apresenta valores médios do rendimento obtidos por um grande número de bombas comerciais em função da rotação específica (velocidade específica) e da vazão.
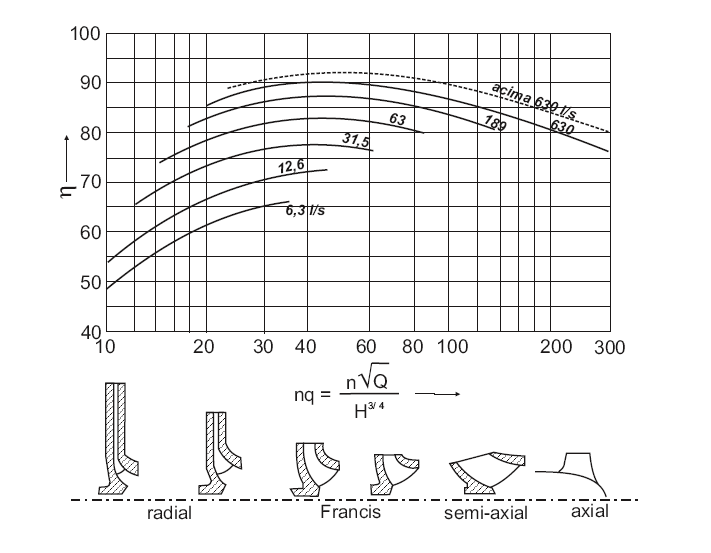
Outras consultas podem ser feitas nas páginas: