4.7 Modelo - m

É o fenômeno ensaiado em laboratório, que geralmente é a representação do fenômeno em escala não natural.

4.8 Protótipo - p

É o fenômeno do qual desejamos obter as informações sem recorrer a ensaios, geralmente representa o fenômeno na escala real.

Para viabilizar o mencionado anteriormente, devemos ter, tanto o modelo como o protótipo, definidos pela mesma função característica, o que equivale a dizer que ambos serão caracterizados pelos mesmos números adimensionais, sendo este fato denominado de condição de semelhança.

4.10 Condição de semelhança Completa

Para que possamos obter as informações do protótipo (fenômeno não ensaiado), através das informações obtidas no ensaio do modelo, ambos devem ser caracterizados pela mesma função características, o que equivale a dizer, que tanto o protótipo, como o modelo, serão definidos pela mesma função equivalente W [W (π₁ , π₂ , π₃ ....)=0].

A condição de semelhança completa estabelece que:

π_1m = π_1p

π_2m = π_2p

π_3m = π_3p   . . .

 

4.11 Escala de Semelhança

A escala de semelhança de uma propriedade α qualquer é sempre definida como sendo a relação entre α_m e α_p.

Exemplo:

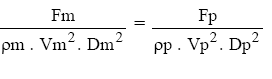
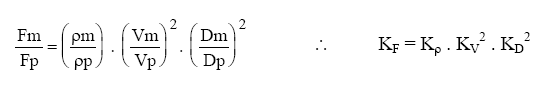
K_F ® escala de força ou escala dinâmica

K_ρ ® escala de massa específica

K_V ® escala de velocidade ou escala cinemática

K_D ® escala de diâmetro ou escala geométrica

4.12 - Adimensionais Típicos das Bombas Hidráulicas

Antes de propor os exercícios, vamos nos deter em uma aplicação bastante importante da análise dimensional para o estudo da mecânica dos fluidos, que é a sua aplicação às máquinas hidráulicas em particular às bombas hidráulicas.

Esta aplicação é comumente usada pelos fabricantes das bombas pelos seguintes motivos:

(1º) - minimizar os custos e otimizar o tempo para ensaios;

(2º) - obter características hidráulicas das bombas, cujas dimensões excedam as permitidas pelas suas bancadas de testes.

As figuras 4.4 a e 4.4 b procuram dar exemplos de bombas reais e bombas em modelo reduzido.

Figura 4.4 a

Figura 4.4 b

A função característica do fenômeno pode ser representada pelas seguintes variáveis:

Nm – potência da máquina hidráulica, no caso N_B potência da bomba;

Dr – diâmetro do rotor;

n – rotação da bomba;

Q – vazão de escoamento do fluido que atravessa a bomba;

γ H_B – variação de pressão estática entre a entrada e saída do fluido, considerando o diâmetro da entrada igual ao diâmetro da saída;

ρ - massa específica do fluido que atravessa a bomba;

µ - viscosidade dinâmica do fluido que atravessa a bomba;

E – elasticidade.

Portanto: f (N_B, Dr, n, Q, γ H_B, ρ, µ, E) = 0.

A partir da função característica conhecida, podemos aplicar o teorema dos π:

(1º) - número de variáveis que causam influência no fenômeno - n=8

(2º) - Equação dimensional de cada uma das

[N_B] = F x L x T^-1

[Dr] = L

[n] = T^-1

[Q] = L³ x T^-1

[γ H_B] = F x L^-2

[ρ] = F x L^-4 x T²

[µ] = F x L^-2 x T

[E] = F x L^-2

(3º) - k - número de grandezas fundamentais envolvidas no fenômeno - k=3

(4º)- m- número de números adimensionais - m = n - k \ m = 5

W ® função equivalente do fenômeno formada só por número adimensionais.

W (π₁,π₂,π₃,π₄,π₅) = 0

(5º) - base dos adimensionais - ρ n Dr.

(6º) - números adimensionais -

π₁ = ρ^x1 . n^x2 . Dr^x3 . γ H_B (I)

π₂ = ρ^y1 . n^y2 . Dr^y3 .Q (II)

π₃ = ρ^z1 . n^z2 . Dr^z3 . N_B (III)

π₄ = ρ^α1 . n^α2 . Dr^α3 . µ (IV)

π₅ = ρ^θ1 . n^θ2 . Dr^θ3 . E (V)

Para obtermos os expoentes dos números adimensionais, procedemos como é mostrado abaixo:

(I) F⁰ L⁰ T⁰ = (F x L^-4 x T²)^x1 . (T^-1) ^x2 . (L)^x3 . F x L^-2

   F⁰ L⁰ T⁰ = F ^x1+1 . L^{-4 x1 + x3 - 2} . T^{2 x1 - x2}

  x1+1 = 0 \ x1 = -1

  2x1 - x2 = 0 \ -2 - x2 = 0 \ x2 = -2

  -4 x1 + α3 - 2 = 0 \ 4 + x3 - 2 = 0 \ x3 = -2 \ π₁ = ρ^-1 . n^-2 . Dr^-2 . γ H_B

  ou ® denominado de coeficiente manométrico.

Analogamente, obtemos:

® denominado de coeficiente de vazão;

® denominado de coeficiente de potência;

® que é um adimensional proporcional ao número de Reynolds;

® denominado de número de Cauchy.

Os números adimensionais mencionados anteriormente poderiam representar as seguintes funções equivalentes:

Por outro lado, devemos lembrar que existe uma relação entre N_B, H_B e Q, já que:

e que o número de Cauchy só deve ser levado em consideração para escoamentos compressíveis; portanto considerando escoamentos incompressíveis, temos:

Onde o efeito do número de Reynolds deve ser considerado sempre que: 

Além disto, podemos recorrer a expressão estabelecida por Moody, onde temos que:

Na prática da engenharia aparece um outro parâmetro de real importância para o estudo de semelhanças de máquinas hidráulica, que é denominado de rotação específica (n_S), que é a rotação da máquina hidráulica quando a mesma apresenta uma carga manométrica unitária e vazão unitária.

Define-se numericamente a rotação específica (n_S) da seguinte forma:

onde Q e HB, e n são consideradas respectivamente em m³/s, m e rpm e lidas no ponto de projeto, aquele onde se tem o η_máxB

Conclusão - Para escoamentos incompressíveis, onde desejamos colher informações para um protótipo (bomba) através de um modelo (bomba), geralmente reduzido, segundo as normas do Hydraulic Institute Standards, devemos ter:

1º - semelhança hidráulica, o que equivale a dizer que a rotação específica, tanto do protótipo, como do modelo, é igual;

2º - semelhança hidrodinâmica, o que equivale a dizer que as dimensões relevantes, como o ângulo da pá, área da garganta, etc. ...devem respeitar a escala geométrica:

A partir destas condições o estudo de semelhança é feito através dos seguintes números adimensionais:

Voltar