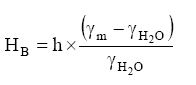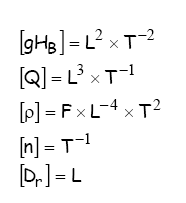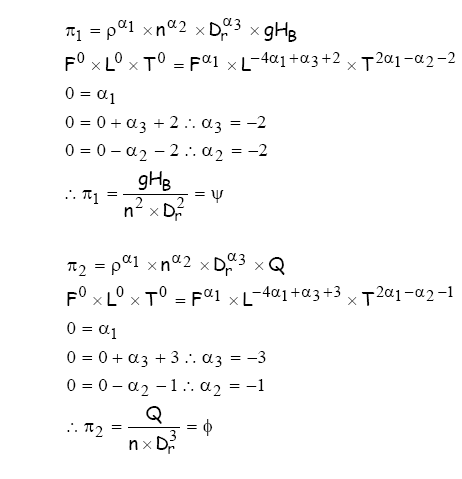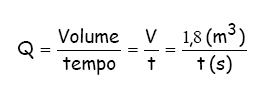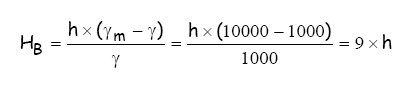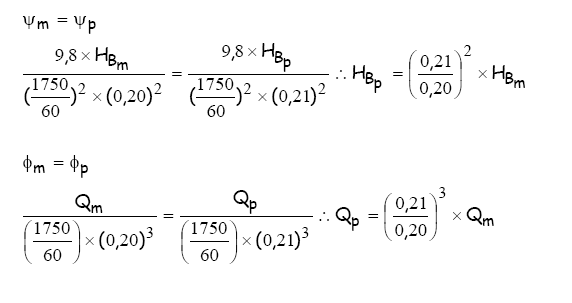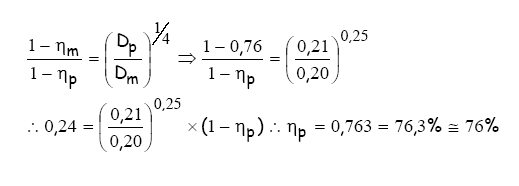|
Neste planejamento considera-se que cada semana tenha quatro (4) aulas |
Iniciamos este encontro relacionando a décima e a décima primeira aula, para
isto evoca-se o exercício 4.14.17:
O
dispositivo representado pela figura (III) foi projetado para ensaiar bombas
centrifugas. Pode-se variar a vazão através da válvula (registro) globo “R”
e medi-la por cronometragem do tempo de enchimento do reservatório com
volume igual a 1,8 m3, além da medida do correspondente desnível
“h” no manômetro diferencial em forma de U. A instalação foi construída de
tal forma que sejam desprezíveis as perdas de carga na mesma. Para uma bomba
de diâmetro de rotor igual a 20 cm e funcionando a uma rotação igual a 1750
rpm obteve-se a seguinte tabela:

Considerando que a função representativa do fenômeno, possa ser f (gHB, Q,
ρ, n Dr) = 0 ; pede-se :
(a)
Os adimensionais característicos do fenômeno;
(b) A
curva universal [ψ = f (φ)] do fenômeno;
(c) A
curva característica [HB = f (Q)] do modelo;
(d) A
curva característica [HB = f (Q)] para uma bomba hidraulicamente e
hidrodinâmicamente semelhante ao modelo que apresenta um diâmetro do rotor
igual a 21 cm e a mesma rotação do modelo
Observação: o item (d) deve ser construído no mesmo gráfico do item (c).
(e)
Se o rendimento máximo do modelo é 76 %,qual o rendimento máximo do
protótipo.
Dados:

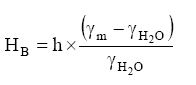
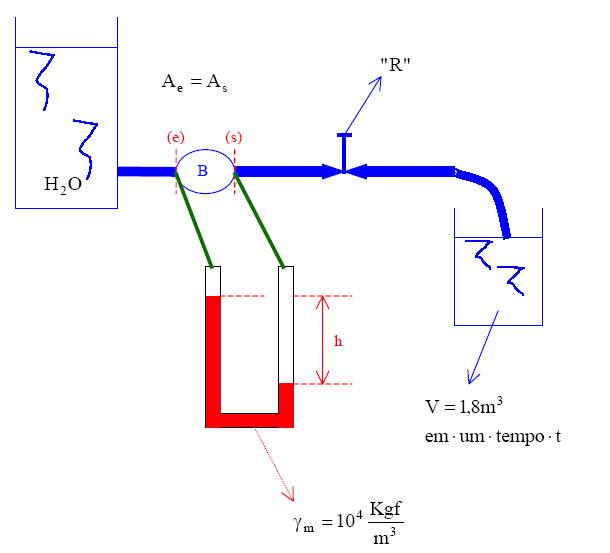
Figura III
Solução do problema proposto:
a)
Aplica-se o teorema dos p:
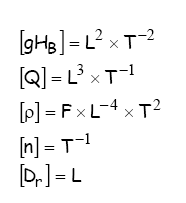
-
determina-se o número de
grandezas fundamentais envolvidas no fenômeno k = 3
-
determina-se o número de
números adimensionais envolvidos no fenômeno m = n - k = 5 - 3 = 2
-
escreve-se os números
adimensionais:
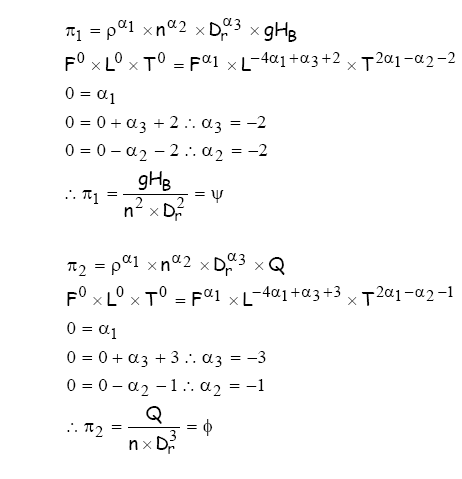
Os
adimensionais anteriores representam respectivamente o coeficiente manométrico
(Y)
e o coeficiente de vazão (f)
os quais permitem obter a curva universal da bomba hidráulica.
b) a
curva universal do fenômeno - Y =
f
(f)
Para que
obtenção da curva universal, além de se estabelecer os dados do modelo, que no
caso são: diâmetro do rotor igual a 20 cm; rotação igual a 1750 rpm, deve-se
evocar conceitos e equações que possibilitem o cálculo da vazão do escoamento
(Q) e da carga manométrica da bomba ensaiada (HB).
Considerando a instalação
hidráulica representada pela figura III, tem-se:
-
pelo conceito da vazão
em volume:
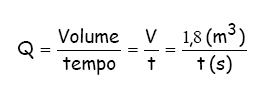
- pela equação
da energia aplicada entre a entrada e saída da bomba:

- pela equação
manométrica aplicada ao manômetro diferencial em forma de U:
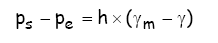
Portanto:
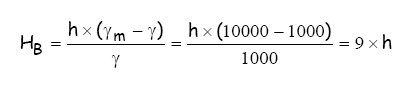
Diante
das informações anteriores, pode-se obter a tabela que dará origem a curva
universal:
|
h (m) |
t (s) |
HB (m) |
Q (m³/s) |
Q (l/s) |
Y |
f |
|
2,2 |
360 |
19,8 |
0,005 |
5 |
5,7 |
2,1E-02 |
|
2 |
180 |
18,0 |
0,01 |
10 |
5,2 |
4,3E-02 |
|
1,7 |
120 |
15,3 |
0,015 |
15 |
4,4 |
6,4E-02 |
|
1,2 |
90 |
10,8 |
0,02 |
20 |
3,1 |
8,6E-02 |
|
0,6 |
72 |
5,4 |
0,025 |
25 |
1,6 |
1,1E-01 |
Com
auxilio do Excel, pode-se obter a curva universal:
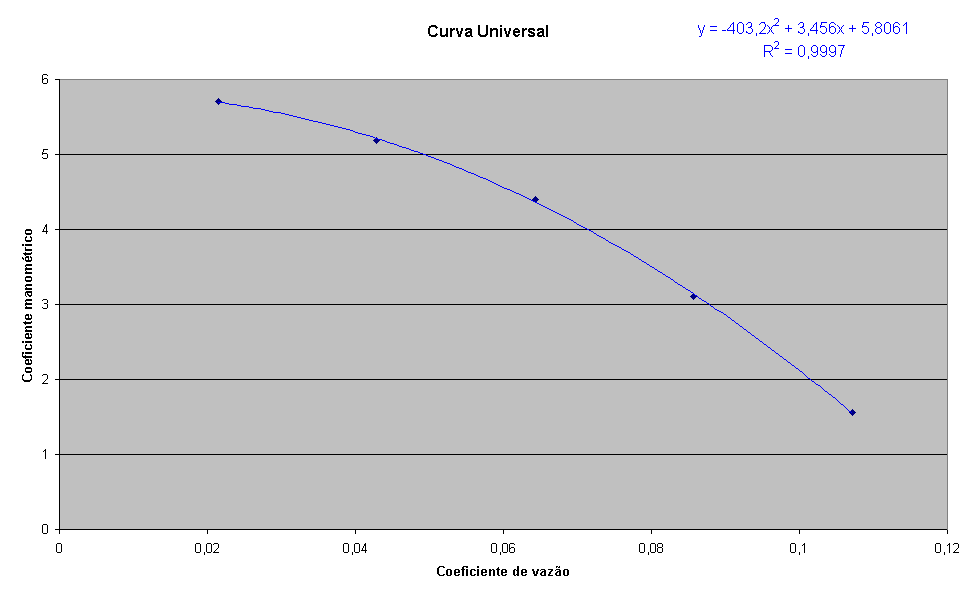
c) a
CCB (Curva Característica da Bomba) do modelo
Através
das equações obtidas no item anterior e também a tabela é possivel obter a CCB
pelo Excel
|
Q (m³/s) |
HB (m) |
|
0,005 |
19,8 |
|
0,010 |
18,0 |
|
0,015 |
15,3 |
|
0,020 |
10,8 |
|
0,025 |
5,4 |
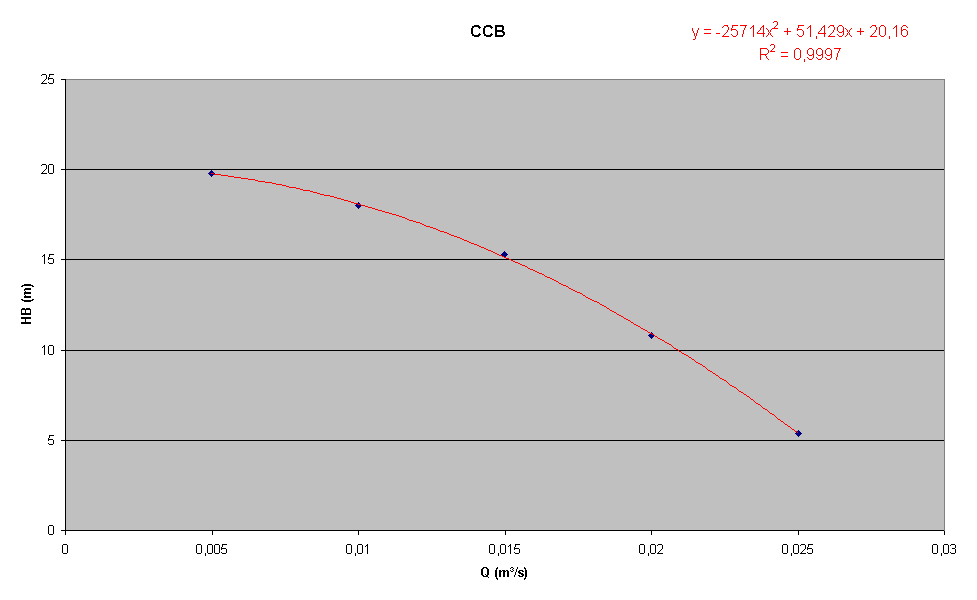
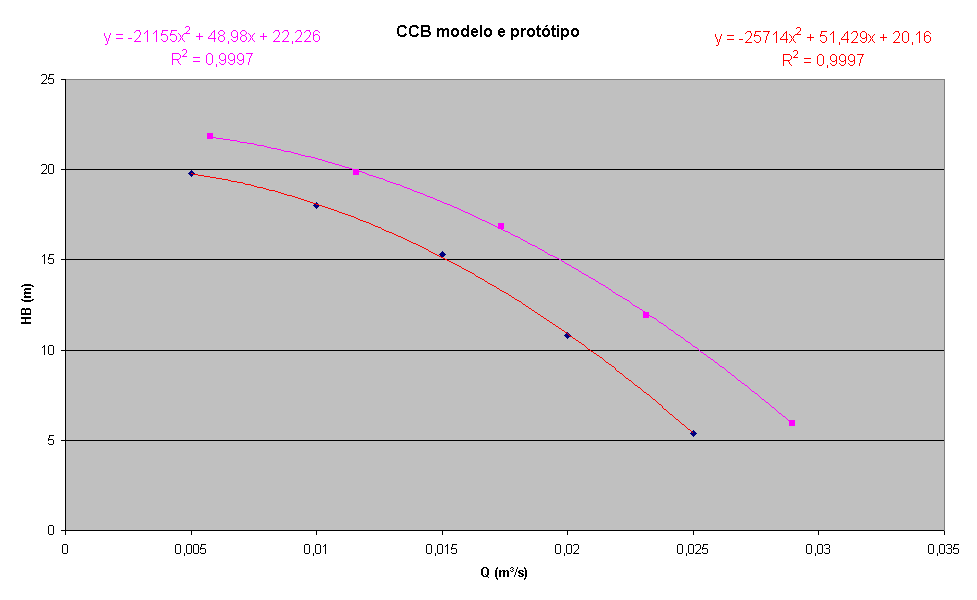
d) A
curva característica [HB = f (Q)] para uma bomba hidraulicamente e
hidrodinâmicamente semelhante ao modelo que apresenta um diâmetro do rotor igual
a 21 cm e a mesma rotação do modelo
Impondo-se as condições de semelhança, tem-se:
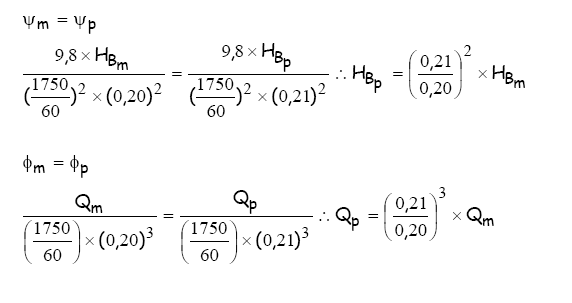
As condições de semelhança resultam:
|
Qp (m³/s) |
HBp (m) |
|
0,0058 |
21,8 |
|
0,0116 |
19,8 |
|
0,0174 |
16,9 |
|
0,0232 |
11,9 |
|
0,0289 |
6,0 |
Com a tabela anterior inserida
na CCB obtida anteriormente pelo Excel, tem-se:
e) Se
o rendimento máximo do modelo é 76 %,qual o rendimento máximo do protótipo.
É
comum se impor que para a condição de semelhança completa o rendimento se mantém
praticamente constante entre modelo e protótipo, porém isto pode se constato
pela equação de Moody:
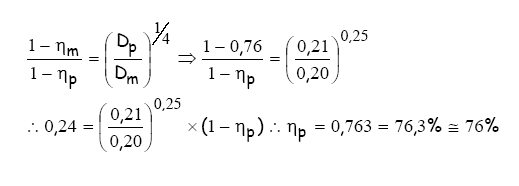
|

Voltar
|
Clique na
figura abaixo para ter acesso a solução anterior em pdf
 |