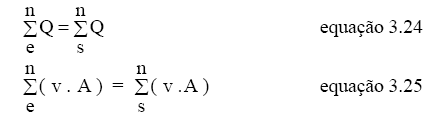3.11 Equação da continuidade ou equação da conservação de massa para o escoamento em regime permanente

Optou-se em apresentar esta equação para duas situações distintas, uma onde o sistema estudado apresenta apenas uma entrada e uma saída, outra onde o mesmo é constituído de várias entradas e várias saídas.

Consideramos a primeira situação, que é representada pela figura 3.11 como sendo um trecho de uma dada instalação.

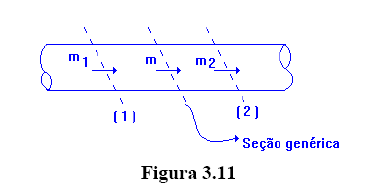
Pela condição de escoamento em regime permanente, podemos afirmar que entre as seções (1) e (2), não ocorre nem acúmulo, nem falta de massa e isto nos permite concluir que: m₁ = m₂ = m = cte

Considerando a conclusão anterior por unidade de tempo, temos: m₁/t = m₂/t = cte, que dá origem a equação da continuidade para esta situação, que é mostrada pelas equações 3.17, 3.18 e 3.19 a seguir:

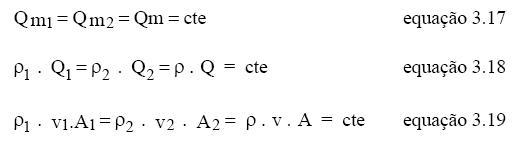
Caso particular: Constituí um caso particular da situação anterior o escoamento incompressível com variação de temperatura desprezível.

Neste caso, temos que a massa específica do fluido permanece constante e a equação da continuidade é representada pelas equações a seguir:

Considerando a segunda situação, onde temos o sistema constituído de diversas entradas e diversas saídas como é mostrado pela figura 3.12.

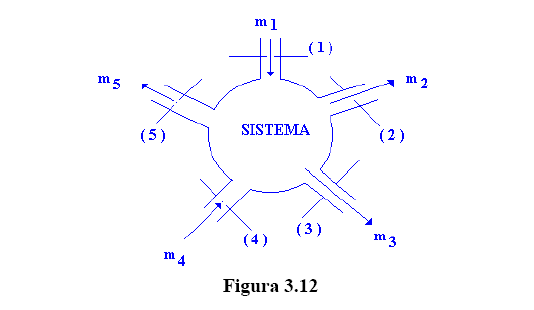
Pela condição do escoamento em regime permanente, podemos escrever que:

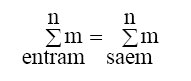
Considerando por unidade de tempo, resulta a equação da continuidade para esta nova situação, que é representada pelas equações 3.22 e 3.23:

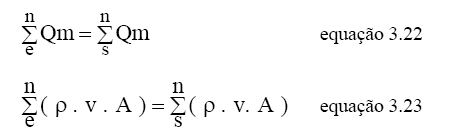
Para a situação descrita pela figura 3.12, temos:

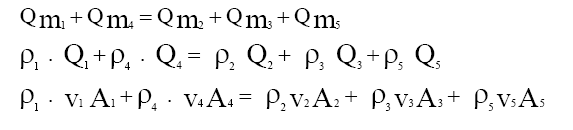
Casos particulares: Consideramos um único fluido entrando, ou vários fluidos entrando, porém neste caso formando-se uma mistura homogênea.

Nestes casos, podemos também escrever a equação da continuidade representada pelas equações 3.24 e 3.25:

Voltar