6.6 Determinação do coeficiente de perda de carga distribuída - "f"

Para a determinação do coeficiente de perda de carga distribuída, "f", inicialmente calcula-se o número de Reynolds, onde:

• se Re for menor, ou igual, a 2000 tem-se o escoamento laminar, para o qual o "f" é determinado pela equação 6.7:

Através da equação 6.7, podemos concluir que o coeficiente de perda de carga distribuída para o escoamento laminar independe do material do tubo, ou seja da rugosidade da parede interna.

• se Re for maior, ou igual, a 4000, temos o escoamento turbulento, que pode ser subdivido em:

• hidraulicamente liso - este regime de escoamento é estabelecido para uma faixa de número de Reynolds variável, onde o limite inferior depende da turbulência natural e o limite superior depende da rugosidade da parede. O escoamento no interior do tubo é turbulento, porém existe próximo a parede interna, devido ao princípio de aderência, uma subcamada (ou filme) laminar, que cobre a rugosidade da parede. Neste caso a parede é denominada de hidraulicamente lisa e o “ f não depende” do material da tubulação.

• hidraulicamente rugoso - este regime de escoamento é estabelecido quando a rugosidade da parede torna-se maior que a espessura da subcamada (ou filme) laminar . Neste tipo de escoamento o diagrama de velocidade aproxima-se do estabelecido para o escoamento ideal, como mostra a figura 6.4.

figura 6.4

Para o escoamento hidraulicamente rugoso o “f” depende somente do parâmetro denominado rugosidade relativa equivalente, que é um adimensional calculado pela expressão representada pela equação 6.8

No caso de Re maior, ou igual, a 4000, podemos determinar o coeficiente de perda de carga distribuída das seguintes formas:

I - maneira analítica → temos duas maneiras para obtenção do “ f ”:

a) método tradicional

a.1) para o escoamento hidraulicamente liso recorre-se a expressão estabelecida por Prandtl-Nikuradse, que é representada pela equação 6.9:

a.2) para o escoamento hidraulicamente rugoso recorre-se, ou a expressão estabelecida por Von-Karman-Nikuradse, que é representada pela equação 6.10, ou a expressão estabelecida por Blench, que é representada pela equação 6.11:

Nota: o escoamento torna-se hidraulicamente rugoso praticamente para:

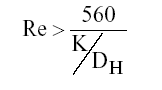
a.3) zona de “transição” entre o escoamento hidraulicamente liso e hidraulicamente rugoso; neste caso, ou recorre-se a equação geral estabelecida por Colebrook-White, que é representada pela equação 6.12, ou pela fórmula ajustada de Wood, que é representada pela equação 6.13:

 

b) método iterativo

Este método é originado da ABNT, onde se recorre as expressões representadas pelas equações 6.14 e 6.15:

Para a utilização das equações anteriores, devemos adotar o seguinte procedimento:

1ª ® Adota-se um erro “E”, por exemplo 10 ^{- 4} .
2ª ® Sendo f = 1/x², adota-se um valor de x_o, que geralmente corresponde a f = 0,02, ou seja, x₀ =1/(0,02)^0,5 , ou seja:

.

3ª ® Através das equações 6.14 e 6.15 calcula-se x.
4ª ®Se o módulo de x- x₀  ≤ E , calcula-se f = 1/x², caso o módulo de x- x₀ > E , adota-se xo = x e repete-se o procedimento.
 

A seguir, mostramos um fluxograma que permite escrever um programa para o cálculo de “ f” para qualquer tipo de escoamento.

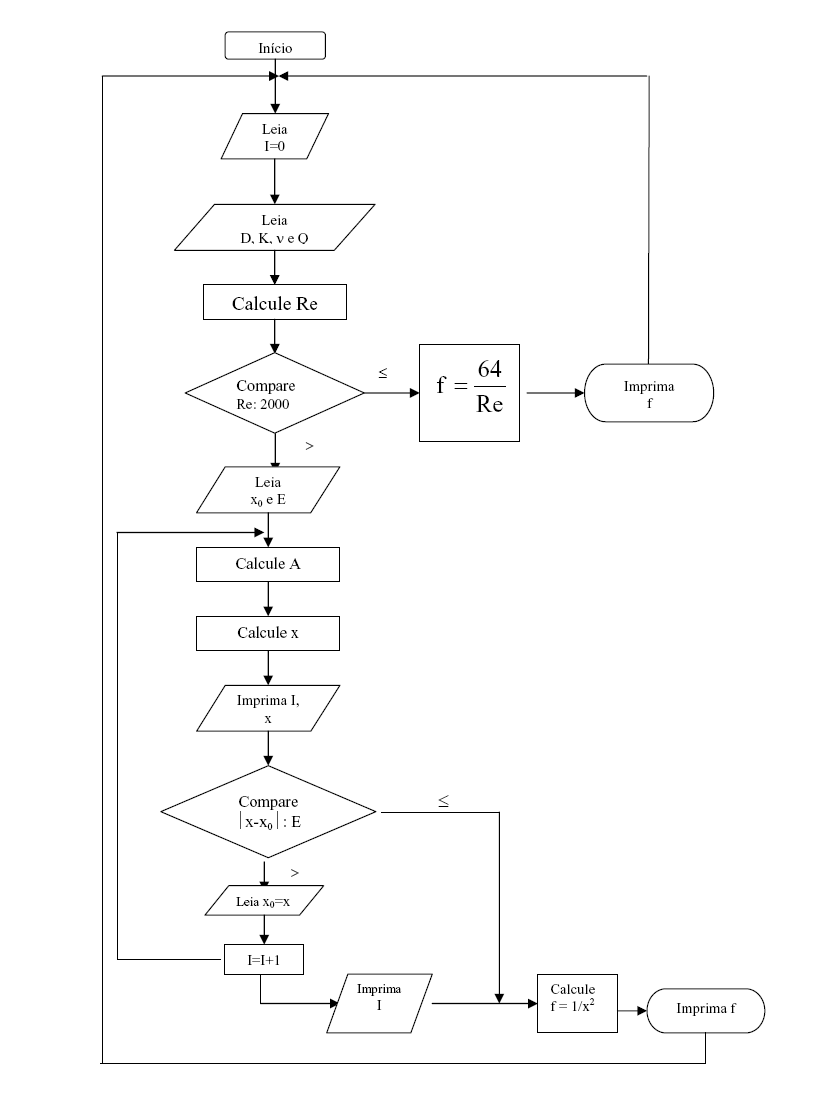
Através do fluxograma, elaboramos um programa em linguagem compatível à máquina de calcular (ou MICRO). Apresentamos a seguir um programa em basic, compatível à máquina de calcular CASIO-PB 700, onde à esquerda simplesmente escrevemos aquilo que se deseja e a direita reescrevemos a linha, porém em BASIC.

II - Através do diagrama de Rouse ou de Moody

Para a utilização deste diagrama, seguimos a seguinte seqüência:

1º → Calculamos o número de Reynolds como mostra a equação 6.16:

onde a viscosidade cinemática é obtida em função do fluido e da sua temperatura. (diagrama 6.2)

2º → Se o Re ≤ 2000, podemos calcular o “ f ” como é mostrado na figura 6.5:

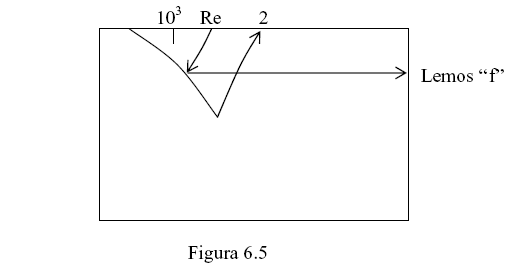
3º ® Se o tubo for considerado liso, marcamos o número de Reynolds (Re) e “levamos” a curva do mesmo até cruzar a curva correspondente ao tubo liso, aí “puxamos” uma horizontal e lemos “ f ” ( Figura 6.6 ).

Figura 6.6

4º ® Se o tubo não for considerado liso, calculamos a rugosidade relativa equivalente (D_H /K). Marcamos o número de Re e “ levamos” sua curva até cruzar a linha do D_H /K calculado, aí “puxamos” uma horizontal e lemos o “ f ” (Figura 6.7).

Figura 6.7

 

III – Determinação experimental (laboratório)

Considere o trecho da instalação hidráulica esquematizada a seguir, onde se sabe que o nível do reservatório levou um tempo “ ∆t” para subir “ ∆h”.
 

São dados:

• L comprimento do tubo entre as seções (1) e (2), que é diferente de zero;

• A_tanque – área da seção transversal do tanque;

• D – diâmetro interno da tubulação;

• os pesos específicos γ e  γ_{m ;}

• o desnível do fluido manométrico h

Aplicando-se a equação da energia e a equação manométrica entre (1) e (2), temos:

Por outro lado, evocando a formula universal, obtemos:

Evocando o conceito de vazão e a equação da continuidade, resulta:

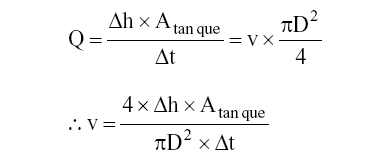
Conhecendo-se a velocidade, podemos determinar o coeficiente de perda de carga distribuída "f".

Nota: Considerando o “f” obtido, reflita como se pode estimar a rugosidade equivalente (K) no laboratório.

 

Voltar