6.3 Classificação da Perda de Carga

6.3.1 Perda de Carga Distribuída → hf ou DH

A perda de carga distribuída é devida a viscosidade e fricção das partículas fluidas entre si e das partículas fluidas com a parede interna do tubo.

O estudo da perda de carga distribuída (hf ou DH) é realizado nas seguintes condições:

a - trecho da tubulação formado só pelo tubo de área de seção transversal constante;

b - comprimento do tubo não desprezível;

c - tubo considerado sem nenhuma obstrução e sem mudanças de direção.

A figura 6.1 representa um trecho de uma instalação, onde entre as seções (1) e (2) só ocorre à perda de carga distribuída.

Instala-se, em cada uma destas seções, um piezômetro que permite a leitura de suas cargas de pressão.

Unindo-se os pontos (A) e (B) por uma reta, temos o que denominamos de linha piezométrica (LP), que é o lugar geométrico que representa a soma das cargas de pressão e potencial.

Aplicando a equação de energia entre (1) e (2) da figura 6.1, temos:

A equação 6.1, permite afirmar que a diferença entre dois pontos da LP representa a perda de carga distribuída no trecho compreendido entre eles.

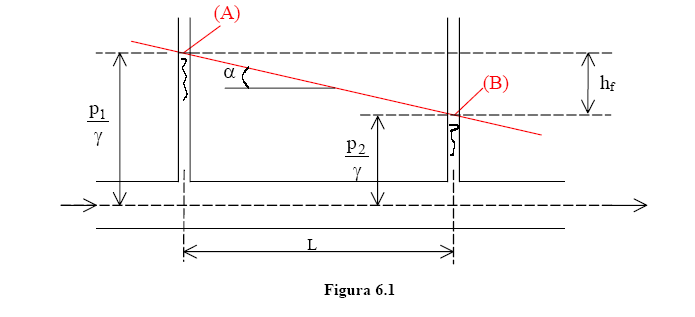
Considerando L, como sendo o comprimento do tubo compreendido entre as seções (1) e (2) e (α) como sendo o ângulo de inclinação da linha piezométrica (L.P), podemos escrever que:

Notas:

1. Em trechos de instalações hidráulicas análogas ao representado pela figura 6.1, podemos afirmar que a linha piezométrica é decrescente no sentido do escoamento.

2. Evocando o conceito da linha de energia (L.E), que é o lugar geométrico que representa a carga total das seções do escoamento, podemos afirmar que a diferença entre a cota da L.E e a cota da L.P nos fornece sempre a carga cinética da seção considerada.

 

6.3.2 Perda de Carga Localizada, ou Singular (h_S)

Não somente a extensão da tubulação, o diâmetro, a velocidade de circulação e a rugosidade, causam perdas no escoamento de fluidos; qualquer acessório que perturbe a velocidade de circulação dele; tais como, o aumento ou diminuição de turbulência, a mudança de direção a variação de velocidade propiciam também uma perda de carga.

Este tipo de perda de carga, que ocorre em um comprimento desprezível em relação ao comprimento da tubulação é denominado de perda de carga localizada, ou singular.

A figura 6.2 mostra a perda de carga que ocorre em uma válvula gaveta.

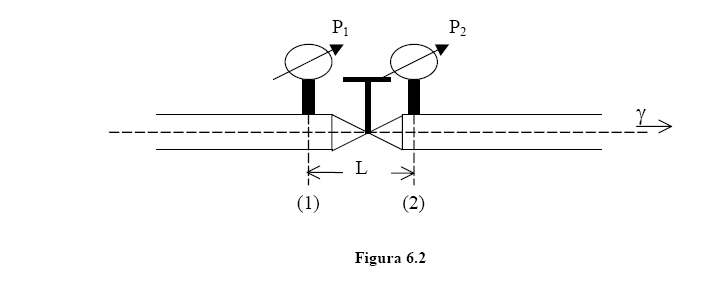
Entre as seções (1) e (2), como o L é desprezível, podemos afirmar que só ocorre h_S, portanto aplicando a equação da energia, temos:

A figura 6.3 representa uma redução de seção, onde também ocorre a perda de carga singular.

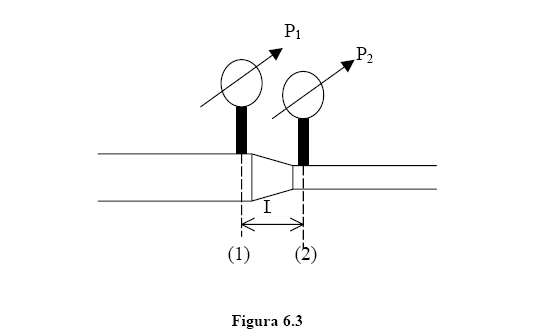
Novamente sabendo que o L é desprezível e aplicando a equação da energia, temos:

Nota:

Na equação 6.4 considera-se que, tanto na seção (2), como na seção (1), o escoamento é turbulento, ou seja, coeficientes de energia cinética iguais e iguais a 1 (α1 = α2 ~ 1,0).

6.4 Cálculo Perda de Carga Distribuída (hf ou ∆H)

Apresenta-se o cálculo da perda de carga distribuída pela chamada fórmula universal, que é originada da análise dimensional (exercício 4.14.23), isto pelo fato da mesma ser válida para qualquer escoamento incompressível e ainda ser reconhecida pela ABNT.

Nota:

No apêndice 6.1 mostramos outra maneira comumente usada para a determinação da perda de carga distribuída, que é através da fórmula de Hazen-Williams.

A equação 6.5, representa a fórmula universal.

onde:

f ® coeficiente de perda de carga distribuída;

L® comprimento do tubo de área de seção transversal constante;

D_H ® diâmetro hidráulico;

v ® velocidade média do escoamento;

g ® aceleração da gravidade, comumente considerada igual a 9,8 m/s²

6.5 Cálculo da Perda de Carga Localizada ou singular (h_S)

A expressão representada pela equação 6.6 (para projetos de instalações hidráulicas muitas vezes não utilizamos esta expressão para o cálculo da perda de carga localizada, mas sim o conceito de comprimento equivalente como mostraremos mais adiante) é usada para o cálculo da perda de carga localizada (singular):

onde:

K_S ® coeficiente de perda de carga singular;

v ® velocidade média do escoamento;

g ® aceleração da gravidade (9,8 m/s²)

 

Nota:

No cálculo de h_S em mudança de seção, geralmente trabalhamos com a velocidade média da seção transversal menor.

Voltar